PODSTAWY MATEMATYCZNE

 

Algebra wektorów

Wektor – obiekt posiadający trzy cechy: wartość, kierunek i zwrot.

Chociaż wektorowi można przypisać punkt przyłożenia, to punkt przyłożenia nie stanowi jego cechy. W opisie wektora istnieje umowa, że jego początek znajduje się w początku układu współrzędnych. Dlatego jednoznaczny opis wektora ogranicza się do podania współrzędnych końca wektora.

W niniejszym podręczniku procesy opisywane są w przestrzeni trójwymiarowej, w układzie kartezjańskim, czyli w układzie trzech wzajemnie prostopadłych osi. Istnieją różne konwencje zapisu takich wektorów. Najbardziej lapidarny opis, to trzy zapisane w odpowiedniej kolejności liczby stanowiące rzuty końca wektora na poszczególne osie. Na przykład: [1,2,3] to wektor, którego koniec posiada następujące współrzędne: x=1, y=2, z=3. Jeżeli wektor ewoluuje, wówczas jego składowe są funkcjami czasu: [x(t),y(t),z(t)]. Można również stosować zapis naturalny, co oznacza, że określony wektor może być przedstawiony jako suma swoich składowych:

W opisie tym litery i-j-k oznaczają wersory, czyli wektory jednostkowe. Wektor jednostkowy to iloraz wektora przez jego wartość.

 

Iloczyn wektorowy

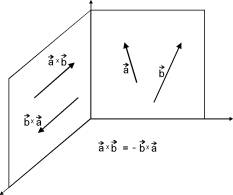
Wynikiem mnożenia wektorowego jest wektor o kierunku prostopadłym do płaszczyzny wyznaczanej przez wymnażane wektory, natomiast zwrot określa się z reguły śruby prawoskrętnej.

Regule prawoskrętnej ulegają też iloczyny wersorów, np.:

Moduł wyniku mnożenia wektorowego to iloczyn wartości wektorów i sinusa kąta pomiędzy nimi. Należy zauważyć, że 

Przykład mnożenia wektorowego:

      

      

 

 

 

 

 

 

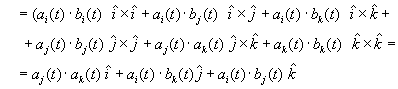
Określanie zwrotu iloczynu wektorowego
dwóch wektorów.

 

 

 

 

 

 

Iloczyn skalarny

Wynikiem mnożenia skalarnego jest wielkość skalarna stanowiąca iloczyn wartości wektorów i cosinusa kąta pomiędzy nimi.

Należy zauważyć, że  , natomiast iloczyny mieszane wersorów wynoszą zero.

 

 

 

Funkcje zespolone

Zespolone liczby, uporządkowane pary liczb rzeczywistych (a, b), w zapisie

dla których zdefiniowana jest relacja równości oraz określone są przemienne i łączne działania dodawania i mnożenie. Element urojony i ma tę własność, że ii=-1, albo

                  

Podczas dzielenia należy dzielną i dzielnik pomnożyć przez sprzężony dzielnik. Liczba sprzężona ’  liczby zespolonej   to

W geometrii na płaszczyźnie liczba zespolona (jako para liczb) jest interpretowana jako wskaz należący do tzw. płaszczyzny zespolonej. Długość tego wskazu, zwana jest modułem liczby zespolonej.

Liczby zespolone zapisywane są w postaci algebraicznej, trygonometrycznej i wykładniczej. Składniki liczby zespolonej mogą być funkcjami, np. czasu.

Przed mnożeniem i dzieleniem liczb zespolonych – warto przekształcić je do postaci wykładniczej

 

 

Iloraz różnicowy

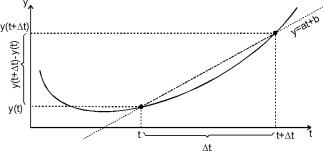
Iloraz różnicowy wyrażony zależnością 11.3 geometrycznie stanowi współczynnik kierunkowy siecznej dwóch punktów na wykresie funkcji f(t), punktów o współrzędnych: [t, f(t)] oraz [t+Dt, f(t+Dt)]

Graficzna interpretacja ilorazu różnicowego a.

 

a=

 

 

 

 

 

 

Pochodna

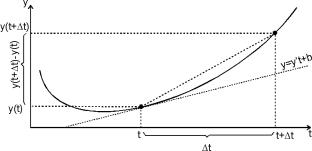
Pochodna stanowi granicę ilorazu różnicowego przy Dt®0 i jest wyrażona zależnością 11.4. Jej geometryczny wyraz to współczynnik kierunkowy stycznej do wykresu funkcji f(t.

Rys. 11.3. Graficzna interpretacja pochodnej y’.

 

y’=

W kinematyce ilorazem różnicowym jest np. szybkość średnia, a pochodną – szybkość.

Przykłady pochodnych funkcji elementarnych:

( a tn )’ = a n tn-1

(sint)’ = cost

(cost)’ = -sint

(et)’ = et

Należy pamiętać o następujących zasadach (obowiązujących gdy funkcje f i g są różniczkowalne, a prawe strony wymienionych niżej relacji posiadają sens matematyczny):

Pochodna sumy (różnicy) dwóch funkcji to suma (różnica) pochodnych.

Pochodna iloczynu funkcji f oraz funkcji g:  (f×g)’=f’×g+f×g’

Pochodna ilorazu funkcji f oraz funkcji g:  (f/g)’=(f’×g - f×g’) /g2

Pochodna funkcji złożonej [F(f(t)]’ = F’×f’

 

Całka nieoznaczona

Obliczanie całki nieoznaczonej to znajdowanie funkcji pierwotnej względem różniczkowania (znajdowania pochodnej). Do wyniku całkowania należy dodać dowolna stałą. Jedną z istotnych w fizyce (szczególnie w dynamice) umiejętności jest identyfikacja fizykalnego znaczenia stałej całkowania. Przykładem całki nieoznaczonej jest szybkość liczona jako całka z wartości wektora przyspieszenia stycznego albo droga jako całka z szybkości.

Przykłady całek funkcji elementarnych:

Należy pamiętać o zasadzie, iż całka sumy (różnicy) dwóch funkcji to suma (różnica) całek tych funkcji, oraz o tym, iż całka z iloczynu dwóch funkcji może być policzona metodą tzw. „przez części”.

 

Całka oznaczona

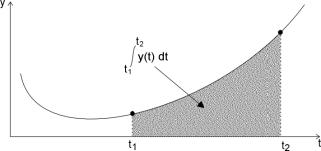
Całka oznaczona z funkcji f(t), czyli liczona w określonych granicach od t1 do t2,  interpretowana jest jako powierzchnia na wykresie tej funkcji ograniczona od góry przebiegiem funkcji, od dołu osią odciętych, a boków - prostymi t = t1 od lewej oraz t = t2 od prawej.

 

Interpretacja geometryczna całki oznaczonej.

 

Przykładem całki oznaczonej jest praca siły F(s) na drodze od s1 do s2.

 

 

 

Zbigniew OTREMBA 2004